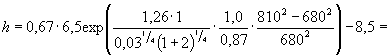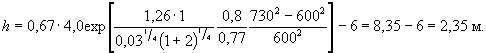Нормативное
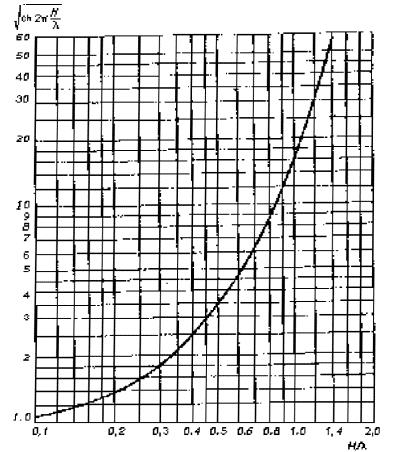
значение показателя текучести грунтов Коэффициент надежности по грунту gg, полученный для оттаявшего монолита, следует принимать в качестве искомого при определении расчетного сцепления талого грунта. А.8 Размывающей (средней на вертикали с глубиной потока Н) скоростью потока υ0 для данного грунта называют минимальную среднюю скорость, при которой появляются первые признаки размыва дна водотока. При отсутствии специальных обоснований размывающую скорость следует определять в предположении, что на пойменных участках дерновой покров отсутствует (разрушен при производстве работ). Размывающую скорость υ0, м/с, для однородного несвязного грунта со средним диаметром частиц d, м, при глубине потока Н, м, рекомендуется определять по формуле где g - ускорение свободного падения (g = 9,8 м/с2). По этой же формуле требуется определять размывающую среднюю скорость υ0D для частиц слоя отмостки и i-го слоя грунта, заменяя в формуле средний диаметр частиц d средними диаметрами частиц соответственно слоя отмостки D и i-го слоя грунта di. Для ускорения расчета по формуле (А.7) рекомендуется пользоваться графиком (рисунок А.1). Для пылеватых песков, содержащих пылеватых частиц (в долях единицы по массе) 0,03 £ pп < 0,20, размывающую скорость следует определять по формуле Для засоленных песчаных грунтов (средний диаметр частиц до 2 мм) размывающую скорость определяют по формулам (А.7) или (А.8) с коэффициентом 0,92. Рисунок А.1 - График для определения размывающей скорости несвязных грунтов А.9 Размывающую скорость для связных грунтов, м/с, рекомендуется определять по формуле где С - коэффициент Шези, определяемый в зависимости от глубины потока Н и коэффициента шероховатости n: можно принимать С = Н1/6 / n. cр - расчетное сцепление, Па. Для ускорения расчета по формуле (А.9) составлен график размывающей скорости при коэффициенте шероховатости n = 0,03 (рисунок А.2). При n ¹ 0,03 значения υ0, полученные по графику, следует умножать на величину 0,03 / n. Рисунок А.2 - График для определения размывающей скорости связных грунтов при коэффициенте абразивности e = 1 и коэффициенте шероховатости n = 0,03 А.10 Для связных засоленных грунтов, содержащих менее 3 % легкорастворимых солей, размывающую среднюю скорость потока следует определять по формуле υ0с = υ0кc, (А.10) где υ0 - размывающая средняя скорость, определяемая по формуле (А.9); кс - понижающий коэффициент, который допускается принимать в зависимости от расчетного сцепления равным: ср × 105 Па £ 0,05 0,01 0,02 0,03 кс 0,92 0,90 0,90 0,75 ср × 105 Па 0,04 0,05 0,075 ³ 0,010 кс 0,72 0,67 0,63 0,59 При содержании в грунте свыше 3 % легкорастворимых солей размывающая скорость должна устанавливаться на основании специальных исследований. А.11 Размывающую скорость для оттаявших связных грунтов следует определять по формуле υ0t = υ0кt, (А.11) где кt - коэффициент уменьшения размывающей скорости потока для оттаявших грунтов по сравнению с талыми, определяемый по таблице А.2, в зависимости от вида криогенной текстуры грунта в мерзлом состоянии и льдистости за счет ледяных включений* (т.е. отношения объема ледяных включений к объему мерзлого грунта). * Указанную льдистость следует отличать от суммарной льдистости (отношение объема льда к объему мерзлого грунта). Таблица А.2 - Значения коэффициента кt
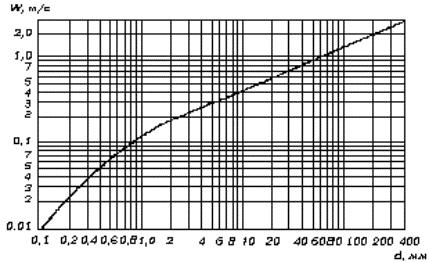
Для оттаявших засоленных грунтов размывающую скорость определяют по формуле υ0tc = υ0кtкc. (А.12) А.12 Гидравлическую крупность частиц несвязного грунта ω (т.е. скорость их осаждения в стоячей воде) следует определять в зависимости от диаметра частиц d по графику (рисунок А.3). Рисунок А.3 - График для определения гидравлической крупности несвязных грунтов Гидравлическую крупность несвязного грунта, состоящего из частиц различной крупности, определяют как средневзвешенную по аналогии с определением среднего диаметра частиц грунта по формуле (А.1) или (А.2). А.13. Гидравлическую крупность отрывающихся отдельностей связного грунта принимают по таблице А.3 в зависимости от их толщины z, определяемой по формуле (5.27). А.14. Для пылеватых песков с содержанием пылеватых частиц pп ³ 0,2 (грунт относится к связному) гидравлическую крупность следует определять по эквивалентному расчетному сцеплению, Па где υ0 - размывающая скорость для песчаных частиц грунта, м/с, определяемая по формуле (А.7); С - коэффициент Шези, м0,5/с; e - коэффициент абразивности, принимаемый равным 1,16 при грядовом движении по руслу песчаного материала, при отсутствии движения песчаного материала e = 1. Если по формуле (А.13) получается cрэ < 0,001 × 105 Па, то рекомендуется принимать cрэ = 0,001 × 105 Па. Таблица А.3 - Гидравлическая крупность отрывающихся отдельностей связного грунта
Приложение Б(обязательное) КОЭФФИЦИЕНТ ФОРМЫ СВАЙНЫХ ФУНДАМЕНТОВБ.1 Под коэффициентом формы М свайного фундамента понимают коэффициент увеличения местного размыва у ряда свай по сравнению с размывом у одной сваи цилиндрической формы. Коэффициент формы М следует определять у расчетного ряда, в качестве которого необходимо принимать один из первых двух рядов свайного фундамента с наибольшей глубиной размыва и расположенного при a £ 20° перпендикулярно продольной оси опоры, а при a > 20° вдоль ее (рисунок Б.1). Рисунок Б.1 - К определению расчетного ряда свайного фундамента: а - продольный вид опоры; б - план свай; 1 - направление течения; 2 - расчетный ряд При одинаковых форме и размерах свай в двух рассматриваемых рядах, а также одинаковых просветах между сваями расчетным будет тот ряд, в котором находится больше свай. Б.2 Коэффициент формы М свайного фундамента с количеством свай n > 1 в расчетном ряду следует определять по формуле где М1 - коэффициент формы отдельной сваи, принимаемый согласно п. 5.1.9; М2с - коэффициент увеличения размыва у двух свай по сравнению с размывом у отдельной сваи Мnс - коэффициент увеличения размыва у n свай по сравнению с размывом у двух свай
S - расстояние в свету между сваями в ряду, м; Шn, Ш2 - полная ширина ряда из n свай и из двух свай (рисунок Б.2). Коэффициент М2с рассчитывают по формуле (Б.2) при всех несвязных грунтах по среднему диаметру частиц d, м; при связных - по утроенной толщине отрывающихся отдельностей (т.е. d = 3z); в слоистых грунтах - по вскрываемому грунту. Значения коэффициентов М2с и Мnс принимают: при M2c £ 1 M2c = Mnc = 1; при M2c ³ 1,75 / M1 M2c = 1,75 / M1; при М2сМnc ³ (1,1 / M1)n2/3 M2cMnc =(1,1 / M1)n2/3. При неодинаковых просветах между сваями в расчетном ряду коэффициенты М2с и Мnс определяют с учетом наибольшего просвета Smax (см. рисунок Б.2) по формулам
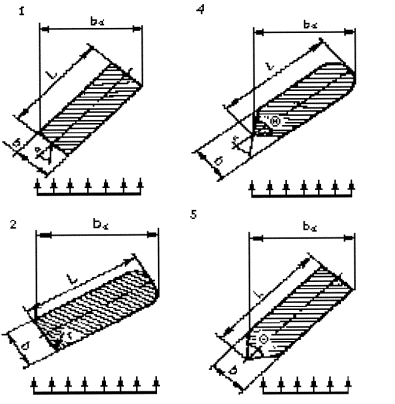
Произведение М2с(max)Мnс(max) необходимо сопоставить с коэффициентом увеличения размыва М2с(min) у двух свай в ряду, расположенных с минимальным просветом Smin. К расчету по формуле (Б.1) следует принимать наибольшее значение из сопоставляемых величин. При этом, если М2с(max)Мnc(max) < Мnc(min), то принимают Мnc = 1. При наличии наклонных свай в плоскости, перпендикулярной направлению сечения, к расчету следует принимать среднюю величину просвета S между ними на уровне выше отметки общего размыва (рисунок Б.3, а), а в случае, когда низ плиты ростверка заглублен ниже отметки общего размыва - расстояние между сваями в месте примыкания к плите ростверка (рисунок Б.3, б). Рисунок Б.2 - Основные геометрические размеры свайных рядов: а - ряд с одинаковыми просветами между сваями; б - ряд с неодинаковыми просветами Рисунок Б.3 - Часть фасада опор с наклонными сваями фундамента Приложение В(справочное) ЗНАЧЕНИЯ ПРИВЕДЕННОЙ ШИРИНЫ ba ХАРАКТЕРНЫХ ФОРМ ОПОРФормулы для определения приведенной ширины ba некоторых характерных форм опор (или их элементов) даны в таблице В.1. Формулы не учитывают возможной скошенности или закругления вершины двугранного угла Q, которыми в расчетах приведенной ширины опоры можно пренебречь. Характерные формы опор представлены на рисунке В.1. Таблица В.1 - Формулы для приведенной ширины опоры
Рисунок В.1 - Характерные формы опор Приложение Г(справочное) ПРИМЕРЫ РАСЧЕТА МЕСТНОГО РАЗМЫВА У ПРОМЕЖУТОЧНЫХ ОПОР МОСТОВПример Г.1 Глубина и средняя скорость перед опорой после общего размыва Н = 6 м и υ = 1,25 м/с. Дно реки сложено мелкозернистым песком, гранулометрический состав которого приведен ниже: Диаметр частиц, мм > 0,1 0,1 - 0,25 0,25 - 0,50 0,50 - 1,00 1 - 2 2 - 3 Содержание pi, по массе, % 2,15 23,61 53,26 16,02 3,57 1,39 Определить глубину местного размыва у овальной в плане опоры шириной b = 4 м и длиной L = 12 м (см. рисунок 5.1). Опора расположена под углом a = 15° к направлению течения. Решение. 1. Определяем неоднородность грунта. Самая крупная фракция составляет менее 2 % массы грунта. Поэтому по формуле (А.4) средний диаметр крупных частиц грунта:
По формуле (А.2) средний диаметр частиц грунта:
Имеем Dmax / d = 2,2 / 0,46 = 4,8, что больше 3, т.е. не соблюдается одно из условий однородности грунта согласно п. А.4. Проверяем второе условие. Размывающая скорость для частиц диаметром 2,2 мм по графику (см. рисунок А.1) υ0Dmax = 1,23 м/с, что меньше скорости течения. Следовательно, грунт в рассматриваемых условиях отмостки не образует, и расчет выполняем как для однородного грунта со средним диаметром частиц 0,46 мм. 2. Поскольку υ > υ0 (так как даже υ > υ0Dmax) глубину местного размыва определяем по формуле (5.1), в которой неизвестны параметры υв, M и K. 3. При гидравлической крупности грунта со средним диаметром частиц 0,46 мм ω = 0,06 м/с (см. рисунок А.3) и взмучивающая скорость по формуле (5.7) υв = (9,8 × 0,06 × 6)1/3 = 1,52 м/с. Примечание. Более правильным является определение гидравлической крупности как средневзвешенной по аналогии с определением среднего диаметра частиц грунта по формуле (А.2); тогда получается ω = 0,046 м/с и υв = 1,4 м/с. 4. По п. 5.1.9 коэффициент формы овальной опоры M = 0,85. 5. Для определения коэффициента косины K вначале по приведенным в приложении В формулам получим при a = 15° приведенную ширину опоры: ba = (L - b)sin a + b = (12 - 4)sin 15° + 4 = 6,07 м. По рисунку 5.7 или по формуле (5.13), поскольку ba / b < 2,53M1/3 имеем:
6. Глубина местного размыва по формуле (5.1):
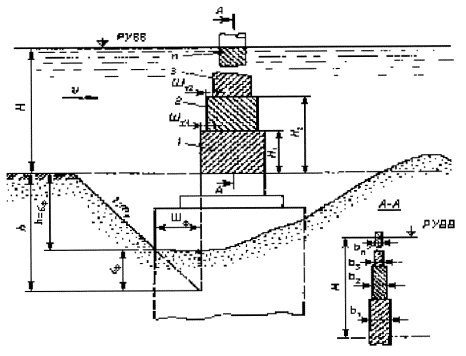
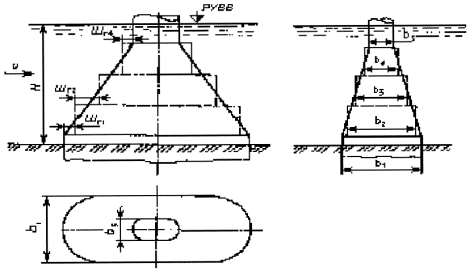
Пример Г.2 Для условий примера Г.1 определить глубину местного размыва у опоры на массивном фундаменте, состоящей из двух элементов овальной формы в плане: нижняя часть возвышается над дном на высоту H1 = 2,0 м, как в примере Г.1 (b1 = 4 м, L1 = 12 м), верхняя имеет b2 = 3 м и L2 = 11 м (см. рисунок 5.2, б). Решение. Расчет местного размыва производим по формуле (5.3), в которой неизвестен только параметр F(b), учитывающий геометрию опоры. 1. Элементы опоры в плане овальной формы, поэтому они имеют одинаковый коэффициент формы М1 = М2 = 0,85 (см. п. 5.1.9). 2. Коэффициент косины для первого элемента определен в примере Г.1 и равен K1 = 1,22. Аналогично для второго элемента bα2 = (11 - 3)sin 15° + 3 = 5,07 м;
3. По формуле (5.11) при Н1 / Н = 2 / 6 = 0,334 > 0,3 А1 = 1 и j1 = 1/3 f1
= По формуле (5.12), в которой Аn-1 = А2 = А1 и j2 = j1, f2 = 1 - 0,695 = 0,305. 4. По формуле (5.5) F(b) = 40,6 × 0,85 × 1,22 × 0,695 + 30,6 × 0,85 × 1,39 × 0,305 = 1,65 + 0,70 = 2,35. 5. Подставляя в формулу (5.3) результаты проведенного расчета и полученные в примере Г.1, определим глубину местного размыва: h =
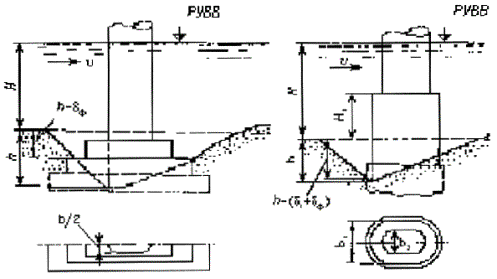
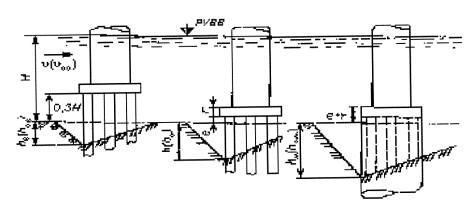
0,77 × 6,00,4 Пример Г.3 Для условий примера Г.1 определить глубину местного размыва у опоры на свайном основании (см. рисунок 5.4, а и б): Число свай-оболочек диаметром b1 = 1,2 м по фасаду n = 2, просвет по фасаду между сваями S = 1,5 м; плита ростверка прямоугольной формы в плане, шириной по фасаду b2 = 5,0 м и длиной L2 = 12 м; низ плиты ростверка расположен выше отметки дна после общего размыва на е = 0,5 м, толщина плиты ростверка r = 1,5 м; тело опоры овальной формы в плане, шириной и длиной соответственно b3 = 3 м и L3 = 11 м. Решение. Поскольку е < 0,3Н, расчет глубины размыва следует производить по формуле (5.6). Расчет сводится к определению глубины размыва hе у опоры при положении низа ростверка относительно дна после общего размыва, равном е = 0,3Н (см. рисунок 5.5, а), и глубины размыва hм у опоры на массивном фундаменте, по форме в плане соответствующей плите ростверка и с отметкой верха, равной отметке верха плиты (см. рисунок 5.5, в). Для указанных глубин размыва постоянным является параметр, характеризующий гидравлические характеристики потока. F(Н, υ) = 0,77Н0,4 Для проводимых расчетов глубин размыва общими являются также коэффициенты формы и косины элементов опор. 1. Коэффициент формы свайного основания определяем по приложению Б: - коэффициент формы отдельной сваи цилиндрической формы М = 1 (см. п. 5.1.9); - коэффициент увеличения размыва у двух свай по сравнению с размывом у отдельной сваи по формуле (Б.2):
что меньше 1,75, поэтому полученную величину принимаем за искомую. По формуле (Б.1) коэффициент формы свайного фундамента или 1-го элемента опоры М1 = 1 × 1,65 = 1,65. Коэффициент косины свайного основания следует принимать K1 = 1 (см. п. 5.1.10). 2. Коэффициент формы плиты ростверка (или массивного фундамента) М2 = 1,24 (см. п. 5.1.9). Приведенная ширина плиты ростверка (или массивного фундамента) по приложению В bα2 = L2sin 15° + b2cos 15° = 12sin 15° + 5cos 15° = 3,11 + 4,82 = 7,93 м. При 3. Коэффициенты формы и косины тела опоры (овальной формы) равны соответственно М3 = 0,85 и K3 = 1,39 (получено в примере Г.2). 4. Для опоры на свайном основании при е = 0,3Н = 0,3 × 6 = 1,8 м весовые коэффициенты элементов опоры равны: - для свайного основания при А1 = 1 и j1 = 1/3 по формуле (5.11)
- для плиты ростверка по формуле (5.10) при Аi-1 = Ai = 1, ji-1 = ji = 1/3, Hi-1 = 1,8 м и Hi = 0,3H + r = 1,8 + 1,5 = 3,3 м f2 = - для тела опоры по формуле (5.12) f3 = 1 - 0,82 = 0,18. 5. Параметр F(b) для опоры на свайном основании при е = 0,3Н по формуле (5.5) F(b) = 1,20,6 × 1,65 × 1 × 0,67 + 5,00,6 × 1,24 × 1,1 × 0,15 + 3,00,6 × 0,85 × 1,39 × 0,18 = 1,235 + 0,54 + 0,41 = 2,185. Глубина местного размыва у такой опоры hе = F(Н, υ) F(b) = 1,43 × 2,185 = 3,12 м. 6. Опора на массивном фундаменте имеет два элемента: фундамент и тело опоры. Весовой
коэффициент фундамента при Весовой коэффициент тела опоры по формуле (5.12) f2 = 1 - 0,695 = 0,305. 7. Параметр F(b) для опоры на массивном фундаменте по формуле (5.5) F(b) = 50,6 × 1,24 × 1,1 × 0,695 + 30,6 × 0,85 × 1,39 × 0,305 = 2,5 + 0,69 = 3,19. Глубина размыва у такой опоры hм = 1,43 × 3,19 = 4,56 м. 8. Искомая глубина местного размыва по формуле (5.6) h =
3,12 + (4,56 - 3,12) Пример Г.4 Для условий примера Г.2 определить глубину местного размыва у опоры, если известно, что в русле, коэффициент шероховатости которого n = 0,028, на глубине D = 1 м ниже отметки общего размыва залегают глины с расчетным сцеплением ср = 0,09 × 105 Па. Решение. 1. Вначале определим по формуле (А.9) или графику (см. рисунок А.2) размывающую скорость для глин с расчетным сцеплением ср = 0,09 × 105 Па при глубине потока Н = 6 (при определении размывающей скорости глубина потока отсчитывается от отметки общего размыва независимо от того, на какой отметке ниже общего размыва залегает рассматриваемый грунт). По графику (см. рисунок А.2) размывающая скорость определена равной 1,4 м/с. Поскольку шероховатость русла отличается от той, для которой составлен график (n = 0,03), то фактическая размывающая скорость согласно п. А.9 будет равна υ0 = 1,4 · 0,03 / 0,028 = 1,5 м/с. 2. По таблице А.3 получим две другие необходимые характеристики связного грунта: толщину отрывающихся отдельностей z = 0,87 мм и гидравлическую крупность этих отдельностей ω = 0,12 м/с. Тогда по формуле (5.7) взмучивающая скорость равна υв = (9,8 × 0,12 × 6,0)1/3 = 1,92 м/с. 3. По формуле (5.8) определим начальную скорость υн, в которой для связных грунтов вместо среднего диаметра частиц несвязного грунта следует принимать (см. п. 5.3.2) d = 3z = 3 × 0,87 = 2,61 мм. Поскольку опора состоит из двух элементов, расчетную ширину опоры для определения начальной скорости найдем по формуле (5.9), в которой b1 = 4,0 м и f1 = 0,695, b2 = 3,0 м и f2 = 0,305 (см. расчет примера 2). b = (4,00,6 × 0,695 + 3,00,6 × 0,305)5/3 = (2,18)5/3 = 3,36 м. При
Полученная начальная скорость принята за искомую, так как υн < 0,9υ0 (см. п. 5.1.6). 4. С учетом того, что коэффициент абразивности e = 1,16, так как в воронку размыва поступают песчаные наносы (см. п. 5.3.2), а параметр F(b) = 2,35 (см. расчет примера Г.2), глубина местного размыва в обнажаемой глине (она будет обнажаться, так как размыв в верхнем слое - песке - больше этого слоя) по формуле (5.26) равна
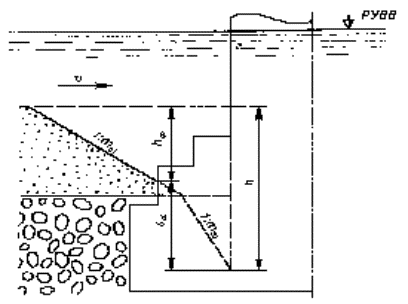
5. При назначении расчетной глубины местного размыва следует учесть следующие два обстоятельства. Во-первых, полученная глубина размыва в глине больше толщины слоя (а в общем случае - слоев) грунта над глиной, т.е. действительно в процессе местного размыва будет обнажаться нижележащий грунт. Во-вторых, согласно п. 5.3.3 полученную глубину размыва следует сравнить с глубиной, сформированной наносами. Из примера Г.2 эта глубина равна 3,28 м, что больше рассчитанной для глины. Поэтому искомая глубина h = 3,1 м. Для рассматриваемого случая, если бы не удовлетворялось первое условие (глубина местного размыва в глине была бы меньше толщины слоя над глиной, т.е. h < D), то к расчету следовало бы принимать глубину местного размыва h = D (отметка дна воронки размыва равна отметке поверхности глин). Приложение Д(рекомендуемое) УМЕНЬШЕНИЕ ГЛУБИНЫ РАЗМЫВА dт ЗА СЧЕТ СТУПЕНЕЙ НА ГРАНИЦЕ ЭЛЕМЕНТОВ ПРОМЕЖУТОЧНОЙ ОПОРЫ, НАХОДЯЩИХСЯ ВЫШЕ ОТМЕТКИ ОБЩЕГО РАЗМЫВАВ тех случаях, когда выше отметки общего размыва опора имеет ступенчатую форму, можно учесть уменьшение глубины местного размыва, обусловленное наличием ступеней тела опоры или фундамента. Фактическая глубина размыва будет равна Уменьшение размыва от n-го элемента опоры (см. рисунок 5.3) за счет (n - 1) ступеней, находящийся ниже этого элемента, следует определять по формуле:
где F(b)n - параметр, определяемый по формуле (5.5) для всех элементов опоры; f(b)n = bn0,6MnKnfn - параметр, учитывающий геометрию n-го элемента опоры;
m0 - коэффициент заложения откоса с верховой стороны воронки, определяемый по таблице Д.1. Таблица Д.1 - Коэффициент заложения откоса m0 верховой стороны воронки
При учете влияния ступенчатой формы опор на глубину размыва коэффициент m0 следует назначать для всех несвязных грунтов по среднему диаметру (крупности) частиц d, а при слоистом залегании грунтов - по верхнему слою грунта, в качестве которого при движении наносов принимают грунт, влекомый потоком. Общее снижение размыва от (n - 1)-го элемента опоры (от второго до n-го) за счет ступеней в пределах глубины потока равно сумме уменьшения размыва, приходящегося на каждый элемент опоры:
или Если окажется, что удовлетворяется условие где то все, что находится выше (к - 1)-й ступени в расчет размыва вводить не требуется. Расчет местного размыва в этом случае производят в предположении, что часть опоры выше (к - 1) ступени отсутствует, и в формуле (5.5) f(b)к, f(b)к+1 ... f(b)n-1 и f(b)n следует принимать равным нулю (см. пример Д.2). При недискретном изменении сечения опоры в плоскости, в которой определяют ширину ступеней, такое сечение следует заменить эквивалентным по площади не менее чем тремя одинаковыми по высоте элементами постоянной ширины (см. рисунок 5.6). Примечание. При расчете глубин местного
размыва слияние ступеней, расположенных на глубине потока выше 0,5Н и имеющих ширину Пример 1. Для условий примера Г.2 определить глубину hт местного размыва у опоры с учетом уменьшения размыва за счет ступени шириной Шт1 = 0,5 м на границе 2-го и 1-го элементов опоры. (Глубина размыва без учета ступеней равна 3,28 м). Решение. 1. Из примера Г.2 известно, что параметры, учитывающие геометрии всей опоры и только второго элемента соответственно равны F(b)2 = 2,35 и f(b)2 = 0,7. Для песка со средним диаметром частиц 0,46 мм принимаем по таблице Д.1 коэффициент заложения откоса m0 = 1,65. 2. Подставляя в формулу (А.2) выявленные выше параметры, получим уменьшение размыва от второго элемента опоры за счет ступени на границе элементов опоры:
Искомая глубина местного размыва по формуле (Д.1) hт = 3,28 - 0,1 = 3,18 м. Как и следовало ожидать, при относительной ширине ступени Шт1 / b2 = 0,5 / 3 << 0,5 влияние ее на размыв незначительное. Пример Д.2. Для условий примера Д.1 определить глубину местного размыва у опоры, если ее второй (верхний) элемент представляет собой стойку цилиндрической формы (коэффициенты формы и косины М2 = K2 = 1) шириной b2 = 1,0 м, а ширина ступени Шт1 = 1,5 м. Решение. 1. Для такой опоры f(b)2 = 1,00,6 × 1 × 1 × 0,305 = 0,305 и соответственно F(b)2 = 40,6 × 0,85 × 1,22 × 0,695 + 1,00,6 × 1 × 1 × 0,305 = 1,65 + 0,305 = 1,955 м0,6. 2. По формуле (5.3) глубина местного размыва (без учета влияния ступени) h =
0,77 × 60,4 3. Для учета
влияния на размыв ступени проверяем условие (Д.4), в котором h2 = 0,77 × 60,4 Поскольку условие соблюдается (1,5 > 0,44 × 1,65), то при расчете местного размыва в F(b)2 по формуле (5.5) f(b)2 = 0 т.е. F(b)2 = f(b)1 = 1,65. 4. Искомая глубина местного размыва по формуле (5.3) hт = 0,77 × 60,4 Тот же результат получается по формуле (Д.1): hт = 2,79 - 0,44 = 2,35 м. Приложение Е(рекомендуемое) УМЕНЬШЕНИЕ ГЛУБИНЫ РАЗМЫВА dф ЗА СЧЕТ ОБНАЖАЕМОЙ В ПРОЦЕССЕ МЕСТНОГО РАЗМЫВА ЧАСТИ МАССИВНОГО ФУНДАМЕНТАЕсли в процессе местного размыва обнажается часть массивного фундамента, размеры которого в плане больше соответствующих размеров опоры, то такой фундамент уменьшает наибольшую глубину местного размыва h на величину dф. Фактическая глубина размыва будет равна hф = h - dф. Глубину dф следует определять (рисунок Е.1): - в грунтах с одинаковыми физико-механическими свойствами при соблюдении неравенства tmax + Шф / m0 £ h - по формуле dф = Шф / m0; - в тех же грунтах при несоблюдении указанного неравенства или при слоистом залегании грунтов - графическим путем. Здесь tmax - глубина заложения (ниже отметки общего размыва) верха наиболее удаленной от тела опоры ступени фундамента; Рисунок Е.1 - К определению глубины уменьшения размыва dф за счет массивного фундамента в грунтах с одинаковыми физико-механическими свойствами: а - аналитическим способом; б - графическим Рисунок Е.2 - К определению снижения размыва dф в слоистых грунтах Шф - суммарная ширина ступеней фундамента от ближайшей передней (при a £ 20°) или боковой (при a > 20°) грани опоры (или фундамента), располагающейся выше отметки общего размыва; m0 - коэффициент заложения откоса с верховой стороны воронки, определяемый по таблице Д.1 для каждого вскрываемого грунта в процессе местного размыва (рисунок Е.2); для всех несвязных грунтов m0 назначают по среднему диаметру частиц (без учета неоднородности). При определении уменьшения глубины размыва dф графическим путем необходимо (см. рисунки Е.1, б и Е.2): вычертить в масштабе продольное (при a £ 20°) или поперечное (при a > 20°) сечение опоры; отложить наибольшую глубину местного размыва на вертикали, где наиболее удаленная от оси опоры ее грань пересекает отметку общего размыва; от полученной таким образом отметки глубины h провести линию верхового откоса, начиная от дна воронки с заложением 1:m0, соответствующем грунту, в котором определялся размыв; при слоистых грунтах заложение откоса 1:m0 в каждом грунте должно соответствовать его физико-механическим свойствам. По отметке пересечения откоса с фундаментом определяют величину dф или непосредственно искомую глубину местного размыва. Примечание. При определении суммарной ширины ступеней фундамента следует: - ширину ступеней принимать без каких-либо поправок на их увеличение вдоль направления потока при косорасположенных опорах; - отсчитывать ширину ступеней фундамента от боковой грани опоры (при любом значении угла a), если ступени с этой стороны уже, чем с передней. Приложение Ж(рекомендуемое) ОПРЕДЕЛЕНИЕ СРЕДНЕГО ДИАМЕТРА ЧАСТИЦ СЛОЯ ОТМОСТКИ И ИХ СОДЕРЖАНИЕ В ГРУНТЕ ПРИ РАСЧЕТЕ МЕСТНЫХ РАЗМЫВОВ У ОПОРВ случае, предусмотренном п. 5.2.4, а, для определения характеристик грунта в слое отмостки D и p поступают следующим образом. Принимают некоторое содержание р ³ 0,02 по массе крупных (отмащивающих) частиц в размываемом грунте и для него подсчитывают средний диаметр частиц D по формуле:
где åpi = p. Принятое значение p и полученную по формуле величину D подставляют в уравнение (5.22). Если окажется p / D > Rp (с точностью ± 5 %), то принимают меньшее значение p, а при p / D < Rp - большее и повторяют те же действия до тех пор, пока подберут значения p и D, удовлетворяющие уравнению (5.22). Если самая крупная фракция со средним диаметром Dmax составляет не менее 2 % массы всего грунта (р ³ 0,02) и удовлетворяет неравенству p / Dmax ³ Rp, то в расчет принимают значения Dmax и p этой фракции. Если получено p < 0,02, то глубину размыва определяют по формулам для однородного несвязного грунта. Пример. Для условий примера Г.1 (Н = 6,0 м, υ = 1,25 м/с, опора овальной формы b = 4,0 м, косина потока a = 15°), определить глубину местного размыва, если в процессе общего размыва обнажился гравий средним диаметром частиц d = 3 мм следующего гранулометрического состава: d, мм 25 - 15 15 - 10 10 - 7 7 - 5 5 - 3 pi, % по массе 1,2 2,4 3,7 6,7 17,2 d, мм 3 - 2 2 - 1 1,0 - 0,5 0,3 - 0,25 0,25 - 0,10 pi, % 31,2 10,8 5,6 17,0 4,2 По руслу влекутся донные наносы - песок со средним диаметром частиц dм = 0,46 мм. Решение. 1. Определим неоднородность грунта. Самая крупная фракция составляет менее 2 % массы грунта. Поэтому по формуле (А.4) средний диаметр крупных частиц:
Имеем Проверяем второе условие. Размывающая скорость для частиц диаметром 17 мм по графику (см. рисунок А.1): υ0Dmax = 2,05 м/с, что больше скорости течения. Следовательно, данный грунт может образовывать отмостку (т.е. он может рассматриваться как неоднородный). 2. Определяем метод нахождения крупности частиц слоя отмостки. Для этого находим: а) начальную скорость для частиц Dmax по формуле (5.8) при υнDmax = 2,05 б) коэффициент абразивности для частиц Dmax при среднем диаметре мелких частиц, в качестве которых следует принимать средний диаметр частиц наносов (см. п. 5.2.3), dм = 0,46 мм, равен emax = 1, так как Dmax / dм = 37 > 30 (см. п. 5.2.3). Неравенство emaxυ > υнDmax удовлетворяется, поэтому средний диаметр частиц слоя отмостки определяем из уравнения (5.22). 3. Задаемся содержанием отмащивающих частиц p = 0,02. Для D = Dmax = 17 мм гидравлическая крупность по рисунку А.3 ωD = 0,5 м/с; при Н = 6 м взмучивающая скорость υвD = 3,05 м/с. По формуле (5.19) при М = 0,85 и K = 1,22 находим глубину местного размыва в однородном несвязном грунте со средним диаметром частиц D = Dmax и скорости потока υ = υ0D = 2,05 м/с h0D = 0,77 × 60,40,40,6
× 0,85 × 1,22 Определяем по (5.23) параметр
т.е. уравнение (5.22) не удовлетворяется и требуется изменить характеристики отмащивающего грунта. 4. Принимаем в качестве отмащивающих частиц три наибольших по крупности фракции. Тогда p = 0,012 + 0,024 + 0,037 = 0,073;
Для принятого грунта имеем: по рисунку А.3 ωD = 0,42 м/с; по рисунку А.1 υ0D = 1,87 м/с; по формуле (5.7) υвD = 2,9 м/с; по формуле (5.8) υнD = 1,87 по формуле (5.19)
с учетом, что 0,77H0,4b0,6MK = 3,75, по п. 5.2.3
при
5. При p = 0,11 D = 9,8 мм. Для такого грунта ωD = 0,41 м/с; υ0D = 1,81 м/с; υвD = 2,8 м/с; υнD = 0,76 м/с; h0D = 3,75
Параметры отмащивающего грунта найдены. Он будет отмащивать воронку, так как υ0D > υ и D / d = 9,8 / 3 = 3,26 > 3. 6. По формуле (5.16) глубина размыва с учетом образования отмостки
7. Согласно п. 5.3.3 полученную глубину размыва необходимо сопоставить с глубиной размыва в грунте, влекомого потоком. Из примера Г.1 эта глубина равна 3,4 м. Следовательно, к расчету надо принимать глубину размыва 3,12 м. Как видим, эффект учета неоднородности грунта невелик, что можно было бы прогнозировать, поскольку отношение D / d близко к 3 (критериальной величине). Глубина размыва в однородном гравии с учетом абразивного воздействия наносов равна 4,98 м, но в этом случае надо было бы принимать к расчету глубину размыва 3,4 м в грунте, влекомым потоком, - песке со средним диаметром частиц 0,46 мм. Приложение И(обязательное) РАСЧЕТ РАЗМЫВОВ У ПРОМЕЖУТОЧНЫХ ОПОР ПРИ СЛОИСТОМ ЗАЛЕГАНИИ ГРУНТОВИ.1 Расчет размывов при слоистом залегании грунтов зависит от взаимного расположения грунтов, вскрываемых в процессе местного размыва. Возможны следующие случаи слоистого залегания грунтов: а) все слои, которые прорезает воронка местного размыва, состоят из однородных несвязных грунтов, причем по мере увеличения глубины местного размыва вскрывается более крупный грунт или все слои состоят из связных материалов; б) имеется два слоя однородного несвязного грунта, причем вскрывающийся в процессе местного размыва второй слой - более мелкий или такой же по крупности, чем вышележащий; в) процесс местного размыва проходит в двух слоях несвязного грунта, причем один или оба неоднородные; г) процесс местного размыва проходит в двух слоях грунта, причем один из слоев - связный грунт; д) общий случай, когда слоев два и более с произвольным расположением в них грунтов, отличающихся друг от друга по физико-механическим свойствам. И.2 Для случая, указанного в п. И.1а, когда поток не влечет донных наносов, глубину местного размыва определяют вначале по формуле (5.4) для обнажаемого грунта в следующем порядке: находят глубину размыва для первого слоя; если полученная глубина размыва захватывает второй слой, расчет проводят для второго слоя, считая, что он выходит на поверхность, и так до тех пор, пока будет найдет слой, в котором размыв прекратится. Если при расчете для какого-либо слоя глубина размыва получается меньше суммы толщин вышележащих слоев, то это значит, что размыв останавливается на поверхности рассматриваемого слоя. И.3 В случае, указанном в п. И.1а, когда поток влечет донные наносы, расчет глубины размыва следует производить в таком порядке: 1) определяют глубину размыва hн в грунте dм, влекомом потоком, по формуле (5.3); 2) определяют глубины размыва для обнажаемых грунтов согласно рекомендациям п. И.2 по формуле где h0i - глубина размыва, определяемая по формуле (5.19) в обнажаемом грунте со средним диаметром частиц di при скорости потока, равной размывающей υ0i для этого грунта; υ0i, υнi - размывающая и начальная скорости для частиц грунта крупностью di, определяемые для глубины потока Н, т.е. для условий, если бы верх этого слоя находился на отметке после общего размыва. Коэффициент абразивности e определяют по формуле (5.20) с учетом воздействия частиц грунта dм на частицы di; 3) выявляют согласно рекомендациям п. И.2 слой грунта крупностью dj, в котором размыв остановился, и соответствующую глубину размыва hj; 4) сопоставляют глубины размыва hн и hj. Если hн £ hj, то к расчету принимают глубину размыва h = hн. Если hн > hj, то к расчету принимают глубину размыва h = hj. И.4 В случае, указанном в п. И.1б, когда поток влечет донные наносы, глубину местного размыва следует определять по формуле (5.3) или (5.6) для грунта верхнего слоя, независимо от того, обнажился или не обнажился нижележащий слой. В случае, когда поток не влечет донных наносов, следует сопоставить глубины местного размыва h1 и (h2 - hd), где h1 - глубина местного размыва, определяемая для грунта со средним диаметром частиц d1 верхнего слоя по формулам (5.4); h2 - то же, но для грунта d2 нижнего слоя; hd - уменьшение глубины местного размыва в нижележащем слое из-за заноса воронки более крупным грунтом верхнего слоя, определяемое по формуле: Здесь D - толщина верхнего слоя; m1, m2 - коэффициенты заложения верхового откоса воронок в грунтах со средним диаметром частиц соответственно d1 и d2 (см. таблицу Д.1). При h1 ³ h2 - hd к расчету следует принимать глубину размыва h = h1. При h1 < h2 - hd к расчету следует принимать глубину размыва h = h2 - hd. В формуле (И.2) при m1h1 ³ m2h2 принимают hd = 0. И.5 В случае, указанном в п. И.1в, если нижележащий слой состоит из однородного несвязного грунта, то неоднородность вышележащего грунта учитывать не следует. В зависимости от значения средних крупностей частиц рассматриваемых двух грунтов расчет проводят согласно п. И.2 при d1 < d2 или п. И.4 (когда поток не влечет донных наносов) при d1 > d2. Если нижележащий слой неоднородный со средним диаметром частиц в слое отмостки D, то расчет местного размыва в этом грунте следует проводить по формулам: а) при eυ ³ υнD и б) при eυ ³ υнD, но где D - толщина верхнего слоя. При расчете глубин размыва, если имеется движение донных наносов, то они учитываются при определении коэффициента абразивности. Дальнейший расчет связан с крупностью вышележащего грунта. Если по среднему диаметру частиц вышележащий грунт мельче обнажившегося, то к расчету принимают глубину размыва по формуле (5.16) или (И.3). При этом следует учитывать рекомендации п. 5.3.3. Если по среднему диаметру частиц вышележащий грунт оказался крупнее обнажившегося, то глубину размыва, полученную по формулам (5.15), (5.16) или по формуле (И.3), уменьшают на hd согласно формуле (И.2), в которой глубину размыва h1 в вышележащем слое определяют по среднему диаметру частиц грунта d1. Вычисленную таким образом глубину размыва h = h2 - hd необходимо сопоставить с глубинами размыва h1 или hн (глубина размыва в наносах, поступающих в воронку при естественной отмостке русла). К расчету принимают глубину размыва, указанную в таблице И.1. И.6. В случае, указанном в п. И.1г, если верхний слой состоит из связного грунта, то расчет размыва следует производить: - при обнажении несвязного однородного грунта - согласно п. И.2 с учетом того, что связный грунт не заносит воронку размыва в несвязном материале; - при обнажении неоднородного несвязного грунта - по формулам (5.15) или (5.16) или по формуле (И.3). Таблица И.1 - Назначение глубины размыва при слоистом залегании грунтов
В случае, указанном в п. И.1г, когда нижний слой состоит из связного грунта, расчет размыва следует производить: - если есть движение наносов, то согласно п. 5.3.3; - если нет движения наносов, то аналогично случаю И.1б (см. п. И.4) с учетом того, что нижележащий грунт не оказывает абразивного воздействия на связный материал нижнего слоя. И.7 В случае, указанном в п. И.1д, расчет размыва следует производить для обнаженного слоя применительно к одному из случаев И.1а - И.1г с учетом следующего: 1) вместо
толщины верхнего слоя D принимают суммарную толщину
слоев 2) засыпают воронку размыва только несвязные частицы. Воронку местного размыва в обнаженном связном грунте засыпают все вышележащие слои несвязных грунтов, размывающая скорость для которых больше, чем для обнажаемого связного материала (с учетом абразивного воздействия на него несвязных частиц). Если j-й грунт несвязный, то воронку в нем засыпают более крупные (по среднему диаметру частиц) вышележащие несвязные грунты. Средний диаметр частиц грунтов вышележащих слоев, которые засыпают воронку размыва, определяют по формуле:
Здесь Di - только те слои несвязного
грунта, в которых di > dj, или при условии 3) уменьшение глубины местного размыва в j-ом слое из-за заноса воронки более крупным материалом верхних слоев определяют по формуле 4) вычисленную
глубину размыва в j-м слое h = hj
- К расчету
принимают глубину размыва, указанную в таблице И.1, в которой принимают h2 = hj, h1
= hj-1, hd = И.8 Пример. Для условий примера Г.1 (глубина и скорость потока Н = 6,0 м, υ = 1,25 м/с, косина набегания на опору овальной формы в плане шириной b = 4,0 м и длиной L = 12,0 м, a = 15°) определить глубину местного размыва у опоры при следующих геологических условиях: - после общего размыва на поверхности оказался однородный гравийный материал со средним диаметром частиц 5 мм; толщина слоя 1,0 м; - ниже - слой глины толщиной 1,6 м с расчетным сцеплением ср = 0,09 × 105 Па; - под глиной - однородный крупный песок со средним диаметром частиц 0,66 мм. В воронку размыва в качестве донных наносов поступает песок со средним диаметром частиц 0,46 мм (как в примере Г.1). Решение. 1. Определим глубину размыва в гравии. Если гидравлическая крупность по графику (см. рисунок А.3) ω = 0,29 м/с, размывающая скорость при глубине потока Н = 6,0 м по рисунку А.1 υ0 = 1,55 м/с, взмучивающая скорость υв = 2,65 м/с. По формуле (5.8)
при При коэффициентах формы и косины опоры М = 0,85 и K = 1,22 (см. пример Г.1) по формуле (И.1) глубина размыва в гравии (e = 1,115, см. п. 5.2.3) h =
0,77 × 6,00,4 × 4,00,6 2. Полученная глубина размыва больше гравийного слоя. Следовательно, размыв будет проходить в следующем слое - глине. По аналогии с данными примера Г.4 для глины с таким же расчетным сцеплением имеем: - размывающую скорость (также принимаем коэффициент шероховатости русла n = 0,028) υ0 = 1,5 м/с; - толщину отрывающихся отдельностей z = 0,87 мм; их гидравлическую крупность ω = 0,12 м/с и взмучивающую скорость υв = 1,92 м/с. При 3z = 2,61 мм и m = 0,895 (см. выше) по формуле (5.8) начальная скорость υн = 1,5 3. Глубина местного размыва в глине по формуле (5.6) при F(b) = 4,00,6 × 0,85 × 1,22 = 2,38 и коэффициенте абразивности e = 1,16 (поскольку по руслу движутся песчаные наносы) h =
0,77 × 6,00,4 4. Гравийный материал будет засыпать воронку, образованную в глине, поскольку (см. п. И.7.2) размывающая скорость гравия υ0 / e = 1,55 / 1,115 = 1,39 м/с больше, чем для глины с учетом абразивного воздействия наносов на эти грунты
При коэффициентах заложения откоса воронки для гравия m1 = 1,45 и глины m2 = 1,0 (см. таблицу Д.1), толщине слоя гравия D = 1,0 м и соответствующих глубинах местного размыва в глине из-за заноса воронки гравием равно
поэтому принимаем hd = 0. Тогда фактическая глубина размыва в глине h2 - hd = 3,2 м. Полученная глубина размыва больше суммарной толщины слоев гравия и глины 1,0 + 1,6 = 2,6 м, поэтому вскрывается нижележащий грунт - песок, в котором будет происходить размыв. 5. Для песка со средним диаметром частиц 0,66 мм имеем (по аналогии, как для гравия): ω = 0,08 м/с; υ0 = 0,92 м/с; υв = 1,67 м/с и υн = 0,28 м/с. По формуле (5.2) глубина размыва в песке
6. Полученная глубина размыва больше толщины слоев над вскрываемым грунтом (песком), поэтому указанный грунт будет участвовать в процессе местного размыва. В то же время вышележащие слои (включая сюда и донные наносы) могут оказывать влияние на формирование глубины размыва: - во-первых, более крупный (гравийный) грунт верхнего слоя будет уменьшать глубину размыва в песке (гравий будет ссыпаться в воронку размыва); - во-вторых, поступающие в воронку размыва наносы также могут уменьшить глубину размыва. 7. Занос воронки будет происходить только гравийным материалом (отрываемые отдельности глины будут уноситься потоком). При коэффициентах заложения откосов воронки для гравия m1 = 1,45 и нижележащего слоя песка m2 = 1,6 (см. таблицу Д.1), толщине слоя гравия D = 1,0 м и соответствующих глубинах местного размыва h1 = 2,57 м и h2 = 3,7 м по формуле (И.2) уменьшение глубины местного размыва в песке из-за заноса воронки гравием равно
Соответственно h2 - hd = 3,7 - 1,65 = 2,05 м. 8. Полученная глубина размыва в песке с учетом заноса гравием оказалась меньше и глубины размыва в заносимом материале (2,57 м), и суммарной толщины слоев гравия и глины (2,60 м). Поэтому, если бы поток не влек донные наносы, к расчету следовало бы принимать глубину размыва до отметки верха песка (2,60 м). Так как поток влечет наносы, то следует сопоставить полученную глубину размыва 2,60 м с глубиной, которую формируют донные наносы. Из примера Г.1 известно, что эта глубина размыва равна 3,4 м, что больше полученной. Следовательно, окончательно расчетная глубина местного размыва в рассматриваемых условиях равна 2,60 м. 9. Следует обратить внимание на казалось бы парадоксальное обстоятельство: если бы не было слоя глины, глубина размыва (принципиально) оказалась бы меньше принятой, т.е. h = 2,57 м. Эту глубину следует назначать согласно таблице И.1 (при дополнительных условиях h2 - hd < h1 и h2 > h1). Такой «парадокс» объясняется тем, что при вскрыше нижнего песчаного слоя размеры воронки в плане значительно превосходят эти размеры при формировании воронки в связном материале (коэффициент заложения откосов воронки в глине и песке соответственно равны 1,0 и 1,6). Поэтому и больший объем гравия в первом случае будет засыпать воронку. Приложение К(рекомендуемое) ЗНАЧЕНИЕ КОЭФФИЦИЕНТА Kt ПРИ ОПРЕДЕЛЕНИИ РАЗМЫВОВ У ДАМБ И КОНУСОВ МОСТАКоэффициент Kt, характеризующий увеличение скорости потока в голове дамбы или в верховой части конуса при длине сооружения вверх по течению от оси подходной насыпи lвф меньше требуемой длины (вылета) lв для плавного его обтекания, следует определять по таблице К.1, составленной по формуле Kt = ехр[0,35l2(1 - lвф / lв)2], где l - требуемое для плавного обтекания отношение полуосей дамбы. Расчетные плановые размеры дамб и конусов рекомендуется определять в плоскости, соответствующей РУВВ - расчетному уровню воды в створе моста. Если при расчете
коэффициента Kt окажется, что Kt
³ 0,75 Таблица К.1 - Коэффициент Kt
Приложение Л(справочное) ПРИМЕР РАСЧЕТА ГЛУБИН МЕСТНОГО РАЗМЫВА У СТРУЕНАПРАВЛЯЮЩЕЙ ДАМБЫ И КОНУСА МОСТАПример. Определить глубину местного размыва у левобережной струенаправляющей дамбы и правобережного конуса. В расчетный паводок коэффициенты стеснения потока подходами на левой пойме dл = 0,42, на правой dп = 0,06; глубина воды у голов дамб в бытовых условиях соответственно Нбл = 2,0 м и Нбп = 2,5 м; средний уклон свободной поверхности потока в районе моста i = 0,0002. Левая пойма сложена суглинком с расчетным сцеплением ср = 2,02 × 105 Па; правая пойма - мелким однородным песком со средним диаметром частиц 0,3 мм. В процессе проектирования мостового перехода определены предмостовой подпор Dhв = 0,25 м и расстояние Х0 = 650 м от моста до вертикали, где устанавливается предмостовой подпор. Плановые размеры левобережной дамбы приняты полученными по расчету (т.е. дамба имеет достаточную длину вылета и хорошо обтекается потоком); крутизна откосов дамбы m = 2. У правого устоя запроектирован конус (учитывая малое стеснение потока на пойме). Ширина его вверх по течению от оси подходной насыпи на уровне УВВ составляет lвф = 25 м, хотя по расчету требуется дамба с длиной вылета lв = 42,5 м и отношением полуосей l = 1,5. Крутизна откосов конуса m = 1,5. Решение. 1. Левая пойма пропускает значительно больший расход воды, чем правая, поэтому с нее надо начинать расчет размывов у дамб. Для этого, в первую очередь, определим глубину Нгл = Нгм и скорость υгл = υгм потока у подошвы головы левобережной дамбы. 2. Глубину потока у подошвы головы левобережной дамбы определим по формуле (6.10) Нгм = 2,0 + 0,25 = 2,25 м. По формуле (6.5) коэффициент Шези (принимаем коэффициент шероховатости русла nр = 0,03) Сгм = 2,251/6/0,03 = 38,3 (м0,5/с). 3. С учетом относительного расхода воды, проходящего на ширине отверстия моста при отсутствии стеснения, QL / Q = 1 - (dл + dп) = 1 - (0,42 + 0,06) = 0,52 и соответственно Q / QL = 1 / 0,52 = 1,925 по формуле (6.9)
4. По формуле (6.8) средний уклон свободной поверхности потока перед мостом, как бы вызванный стеснением левой мощной поймы, iм(м) = 0,0002 + 0,845 × 0,25 / 650 = 0,0002 + 0,000325 = 0,525 × 10-3. 5. По формуле (6.3) скорость потока в голове левобережной дамбы υг(м) = 38,3 6. Для правобережного конуса по формуле (6.10) Нгп = Нгс = 2,5 + 0,25 = 2,75 м. 7. Для определения скорости потока в верховой части правобережного конуса υr(с) по формуле (6.4) предварительно найдем: - по формуле (6.9)
- по формуле (6.8) iм(с) = 0,0002 + 0,092 × 0,25 / 650 = 0,235 × 10-3; - по формуле (6.6) b = 1,55 × 0,68 / Подставляя вычисленные значения в формулу (6.4), получим υг(с) = 0,68 8. Глубину размыва в голове левобережной дамбы определим по формуле (6.1) с учетом того, что ее длина вылета достаточная и она хорошо обтекается потоком (Kl = Kl = 1). Для суглинка с расчетным сцеплением Ср = 0,02 × 105 Па, коэффициенте шероховатости русла nр = 0,03 и глубине потока 2,25 м по графику (см. рисунок А.2) размывающая скорость υ0 = 0,62 м/с. При коэффициенте заложения откоса дамбы m = 2 Km = 0,77 (см. п. 6.1.1). Тогда:
9. Расчет глубины размыва в верховой части правого конуса следует также выполнять по формуле (6.1) с учетом того, что его ширина вверх по течению от оси подходной насыпи составляет lвф = 25 м, тогда как для плавного обтекания требуется lв = 42,5 м. При этом следует, что такой конус будет плохо (т.е. с отрывными течениями и водоворотными зонами) обтекаться потоком и поэтому Kl = 0,85. Из-за недостаточных плановых размеров конуса по таблице К.1 при lвф / lв = 25,0 / 42,5 = 0,59 и требуемом отношении полуосей сооружения l = 1,5 получаем Kl = 1,14. При m = 1,5Km = 0,8 (см. п. 6.1.1). Для мелкого однородного песка со средним диаметром частиц 0,3 мм при глубине потока Нгс = 2,75 м неразмывающая скорость по графику (см. рисунок А.1) υ0 = 0,6 м/с. Тогда
Приложение М(обязательное) РАСЧЕТНАЯ ШИРИНА b БЕРЕГОВЫХ ОПОР И ПОПЕРЕЧНЫХ РЕГУЛЯЦИОННЫХ СООРУЖЕНИЙЗа расчетную ширину b береговых опор следует принимать среднюю ширину под водой (до местного размыва) боковой грани опоры, перпендикулярной направлению потока и выступающей из конуса (рисунок М.1). За расчетную ширину b поперечного регуляционного сооружения следует принимать проекцию его длины l0 на нормаль к насыпи или берегу (рисунок М.2) и определять по формуле где a - угол примыкания поперечного сооружения к насыпи или берегу. Угол a должен отсчитываться от продольной оси сооружения вниз по течению; на криволинейном участке - между осью сооружения и касательной к оси насыпи или линии берега в точке примыкания к ним. Длину поперечного сооружения l0, равную средней длине его продольного сечения под водой, следует определять по формуле где lниз - длина поперечного сооружения понизу вдоль его продольной оси. Рисунок М.1 - Расчетная ширина береговой опоры Рисунок М.2 - План поперечных сооружений: а - при угле примыкания поперечного сооружения a ³ 45°; б - то же, при a < 45°; в - определение угла примыкания на криволинейном участке; 1 - подошва (до размыва) откоса сооружения; 2 - урез воды; 3 - схематизированный контур воронки размыва; 4 - расчетный створ; 5 - вертикаль с наибольшей глубиной размыва; 6 - касательная к линии берега Приложение Н(рекомендуемое) ЗНАЧЕНИЯ КОЭФФИЦИЕНТА Kυ ПРИ ОПРЕДЕЛЕНИИ РАЗМЫВОВ У ПОПЕРЕЧНЫХ СЕЧЕНИЙКоэффициент Kυ, характеризующий поступление наносов в воронку размыва, следует принимать равным: - при расположении поперечного сооружения на пойме, размывах в связных грунтах или при υ £ υ0 Kυ = 1; - при ³ 1,35υ0 и расположении поперечного сооружения в русле Kυ = Kυmax = 0,96(H / d)0,05; (Н.1) - при υ0 < υ < 1,35υ0 и расположении поперечного сооружения в русле Для ускорения определения коэффициента Kυmax по формуле (1) рекомендуется пользоваться следующими данными: Н / d 50 100 200 400 600 Kυmax 2,17 1,21 1,25 1,30 1,31 Н / d 1000 2000 40000 6000 10000 Kυmax 1,35 1,41 1,45 1,48 1,52 Приложение П(справочное) ПРИМЕРЫ РАСЧЕТА РАЗМЫВОВ У ПОПЕРЕЧНЫХ СООРУЖЕНИЙ И БЕРЕГОВЫХ ОПОРПример П.1. Определить глубину местного размыва у шпоры, отжимающей поток на криволинейном русле от насыпи, подошва которой попадает в русло. Русло сложено однородным песком со средним диаметром частиц 0,5 мм; у подошвы насыпи глубина и скорость потока соответственно равны Н = 6,5 м и υ = 1,0 м/с. Шпора запроектирована длиной понизу lниз = 25 м с откосом m = 2; угол примыкания к насыпи a = 35° (см. рисунок М.2). Решение. 1. Вначале согласно приложению М определим расчетную ширину шпоры b. По формуле (М.2) длина шпоры l0 = 25 - 0,5 × 2 × 6,5 = 18,0 м, а по формуле (М.1) b = 18,0sin 35° = 10,3 м. 2. Глубину местного размыва будем определять по формуле (7.1), поскольку b / Н > 1. Предварительно в этой формуле определим: - по формуле (7.4) скорость потока в голове шпоры υг = 1,0 + - по рисунку А.1 размывающая скорость при d = 0,5 мм и Н = 6,5 м, υ0 = 0,87 м/с; - по формуле (Н.2)
при υ0 < υ < 1,35υ0 и Kυmax = 0,96 (Н
/ d)0,05 = 0,96 Kυ = 1 + (1,55 - 1) × (1,0 - 0,87) / (0,35 × 0,87) = 1,235; - при m = 2 согласно п. 6.1.1 Km = 0,77, тогда h =
Пример П.2. Для условий примера П.1 определить глубину местного размыва у такой же шпоры, но устраиваемой для отжима потока от вогнутого берега вровень с берегом. При проходе воды в бровках русла глубина и скорость потока у берега Нбр = 4,0 м и υбр = 0,8 м/с (высота сооружения Н1 = Нбр = 4,0 м). Решение. 1. Уточним расчетную ширину шпоры l0 по формуле (М.2) l0 = 25 - 0,5 × 2 × 4 = 21 м; по формуле (М.1) b = 21sin 35° = 12,05 м. 2. Для условий прохода расчетного паводка (Н = 6,5 м, υ = 1,0 м/с) требуется уточнение скорости потока в голове шпоры υг и весового коэффициента f1, учитывающего снижение глубины местного размыва за счет затопления сооружения. По формуле (7.4) υг = 1,0 + По формуле (5.11) (при 3. Для условий прохода расчетного паводка по формуле (7.1) с учетом коэффициента f1 (см. п. 7.6) глубина местного размыва равна h =
4. Согласно п. 7.6 необходимо определить глубину размыва при проходе потока в бровках русла. По аналогии с проводимыми действиями в примере П.1 имеем: υг = 0,8 + Kυmax = 0,96 Kυ = 1 + (1,5 - 1)(0,88 - 0,77) / (0,35 × 0,77) = 1,20. Тогда по формуле (7.1) h =
5. К расчету следует принимать большую из полученных глубин местного размыва, т.е. 3,36 м. Пример П.3. Для условий, приведенных в примере П.1 (Н = 6,5 м, υ = 1,0 м/с, d = 0,5 мм) определить глубину местного размыва у береговой опоры (устоя), боковые грани которой не обсыпаны конусом. Причем боковая грань, перпендикулярная направлению потока, в плоскости расчетного уровня (УВВ) выступает из конуса на bmax = 10 м (см. рисунок М.1). Решение. 1. Согласно приложению М расчетная ширина опоры равна средней ширине под водой боковой ее грани, т.е. b = bmax / 2 = 5 м. 2. Поскольку b / Н < 1, то глубину местного размыва следует определять по формуле (7.2), в которой известно из примера П.1 Kυ = 1,235 и υ0 = 0,87 м/с. Согласно п. 6.1.1 для вертикальной стенки (m = 0) Km = 1. По формуле (7.3) с учетом b / Н < 1 скорость потока у боковой грани опоры υг = υ = 1,0 м/с. Тогда h = Приложение Р(справочное) ПРИМЕРЫ РАСЧЕТА РАЗМЫВОВ У ПОДОШВЫ НАСЫПИ НА ПРИЖИМНОМ УЧАСТКЕ РЕКИ ОТ ПРОДОЛЬНЫХ ТЕЧЕНИЙ ПРИ ОТСУТСТВИИ И НАЛИЧИИ ВОЛНОВЫХ ВОЗДЕЙСТВИЙПример Р.1. Определить глубину размыва у подошвы насыпи с откосом, попавшим в русло, в расчетный паводок. Глубина и скорость потока соответственно равны Н = 6,5 м и υ = 1,4 м/с. Русло сложено суглинком с расчетным сцеплением ср = 0,07 × 105 Па; поток в русле влечет донные наносы со средним диаметром частиц d = 0,3 мм. Коэффициент шероховатости русла nр = 0,03. Решение. По формуле (8.6) глубина размыва
Согласно п. 8.2б, следует проверить по формуле (8.8) возможность заноса полученной глубины размыва донными наносами
К расчету следует принять глубину размыва h = 0,85 м. Пример Р.2. Для условий примера Р.1 определить глубину размыва у подошвы насыпи от продольных течений при наличии волновых воздействий (расчетная высота волны 0,5 м; средний период волн Т = 1,7 с). Решение. Вначале определим коэффициент x, учитывающий увеличение размыва от продольных течений при наличии волновых воздействий. При плотности частиц грунта r = 2650 кг/м3 (и воды r0 = 1000 кг/м3) по формуле (8.10)
По формуле (8.9)
Подставляя коэффициент x в формулу (8.8), имеем глубину размыва
Примечание. Расчет проведен по формуле (8.8), а не (8.6), поскольку из примера Р.1 выяснено, что глубина размыва у подошвы насыпи определяется динамическим равновесием наносов на этом участке русла. Приложение С(рекомендуемое) ОПРЕДЕЛЕНИЕ ГЛУБИНЫ РАЗМЫВА У ПОДОШВЫ НАСЫПИ ОТ ВОЛНОВЫХ ВОЗДЕЙСТВИЙС.1 При обрушении волны на откос она разделяется на два противоположных по направлению потока (рисунок С.1). Из потока, идущего вверх по откосу, формируется так называемый накат волны; нисходящие струи, достигая неукрепленной подошвы откоса, могут вызвать размыв дна у основания откосного сооружения (насыпи). С.2 Скорость струй, идущих вниз по откосу, убывает с глубиной потока. Максимальную скорость нисходящего потока у подошвы откоса (или максимальную донную скорость υдmax) рекомендуется определять по формуле где hв - расчетная высота волны; l - средняя длина волны; Н - глубина воды у подошвы насыпи, исчисляемая от статистического подпертого уровня воды перед насыпью (ПУВВ), складывается из глубины воды у насыпи до размыва Нб и глубины размыва h. Для определения
значения гиперболического косинуса Формула (С.1) справедлива при коэффициенте заложения откоса m £ 3. При более пологих откосах формула завышает значение максимальной донной скорости. Рисунок С.1 - Схема разрушения волны и формирования воронки размыва: 1 - гребень волны до разрушения; 2 - опрокинутый гребень в момент обрушения волны на откос; 3 - траектория движения частиц воды на гребне волны; 4 - исходящие струи, образующиеся при разрушении волны С.3 Если окажется, что максимальная донная скорость меньше размывающей донной скорости υд(0) для грунтов в основании насыпи, то размыва у подошвы насыпи не будет. Рисунок
С.2 - Значения гиперболической функции При υдmax > υд(0) следует задаться глубиной размыва h, определить максимальную донную скорость υдmax при глубине потока перед насыпью Н = Нб + h и сопоставить с υд(0). Операция повторяется до получения υдmax £ υд(0). С.4 По полученной глубине размыва h задают необходимый объем рисбермы для защиты подошвы насыпи от подмыва. При этом крупность камня в рисберме должна обеспечивать устойчивость от воздействия исходящего с откоса потока при глубине воды у насыпи Н. Для предотвращения размывов у подошвы откосов основание насыпи следует укреплять на ширину не менее глубины воды перед откосом. Пример. Определить возможный размыв и соответственно необходимость укрепления подошвы откоса от волнового воздействия при глубине потока перед насыпью Н = 3,2 м, расчетной высоте и средней длине волны соответственно hв = 0,75 м l = 8,4 м; в основании насыпи - суглинок с расчетным сцеплением ср = 0,04 × 105 Па. Решение. По формуле (С.1) определяем максимальную
донную скорость у подошвы откоса. При 2. По формуле (8.12) эквивалентный диаметр суглинка dэ = 7,5(0,1 + 10 × 0,04) = 3,08 мм, для которого размывающая донная скорость по графику (см. рисунок 8.1) υд(0) = 0,52 м/с. Поскольку υдmax > υд(0), необходимо укрепление подошвы откоса. 3. По графику (см. рисунок 8.1) из условия υд(0) ³ υдmax крупность камня dк, которым можно укреплять подошву откоса, равна dк ³ 20 мм. 4. Для определения размыва у подошвы насыпи без его укрепления поступим следующим образом: - из формулы (С.1) определяем требуемое значение гиперболической функции при υдmax = υд(0) = 0,52 м/с
- по графику (см. рисунок С.2) находим для полученного значения гиперболической функции H / l = 0,63; - определяем глубину потока у подошвы насыпи после размыва Н = 0,63 × 8,4 = 5,28 м; откуда глубина размыва h = 5,28 - 3,2 = 2,08 м. Приложение Т(рекомендуемое) ОПРЕДЕЛЕНИЕ РАДИУСОВ КРИВИЗНЫ ИЗЛУЧИНЫТ.1 Радиус кривизны потока у вогнутого берега или прислоненного откоса насыпи определяют по формуле где rи - минимальный радиус кривизны излучины по оси русла шириной Вр. Т.2 Радиус кривизны потока по оси русла rи, когда поток не выходит из бровок русла, совпадает с радиусом кривизны излучины и может быть определен по формуле где аи - расстояние от середины шага излучины lи до ее вершины по оси русла (рисунок Т.1). Т.3 При выходе воды на пойму радиус кривизны потока rи увеличивается по сравнению с тем же в бровках русла rи(бр) и равен где Нр, Нн - средняя глубина потока и глубина потока у вогнутого берега в рассматриваемом створе русла при проходе расчетного паводка; Нрбр, Нибр - соответствующие глубины потока в бровках русла. При устройстве срезки грунта со стороны выпуклого (противоположного укрепляемому) берега радиус кривизны потока rи при выходе на пойму можно принимать по формуле (Т.3) с коэффициентом 1,1 - 1,2. Т.4 Если между продольной осью насыпи и берегом на входе трассы в русло будет угол более 10°, то для входного участка, составляющего не менее ширины нестесненного русла Вр, радиус кривизны русла rи независимо от уровня воды рекомендуется принимать по формуле (Т.2). Пример. Определить глубину местного размыва у подошвы насыпи (см. рисунок Т.1), возникшего в связи с нарушением естественного хода руслового процесса. Русло шириной Вр = 260 м сложено однородным песком со средним диаметром частиц 0,5 мм; минимальный радиус кривизны излучины по оси русла rи = 600 м. Когда поток достигает бровки русла, средняя глубина в русле Нрбр = 4 м; глубина у вогнутого берега Нибр = 6 м; средняя скорость потока υрбр = 0,8 м/с. При расчетном паводке средние глубина и скорость потока в русле Нр = 6,5 м и υр = 1,0 м/с. Речной откос насыпи крутизной m = 2 укреплен каменной наброской. Решение. 1. Вначале определим радиус кривизны потока по оси русла rи при выходе воды на пойму. При средней глубине потока в русле при расчетном уровне и уровне в бровках русла Нр = 6,5 м и Нрбр = 4 м, а также глубине потока у вогнутого берега (у подошвы насыпи) при расчетном уровне Ни = Нибр + (Нр - Нрбр) = 6 + (6,5 - 4) = 8,5 м по формуле (Т.3)
Рисунок Т.1 - К определению радиуса кривизны потока rи: 1 - направление течения; 2 - ось русла; 3 - конец и начало излучины; 5, 6 - трасса и ее входной участок 2. Радиус кривизны потока у вогнутого берега по формуле (Т.1) r = 680 + 260 / 2 = 810 м. 3. По графику (см. рисунок А.1) размывающая скорость для частиц грунта 0,5 мм и глубине потока Н = Нр = 6,5 м υ0 = 0,87 м/с. 4. Определяем для расчетного уровня (при проходе расчетного паводка) глубину местного размыва у подошвы насыпи по формуле (8.13) при коэффициенте шероховатости укрепления (каменной наброски) n = 0,03 и коэффициенте формы укрепления М = 1 [см. пояснения к формуле (8.13)].
= 0,67 × 6,5 × e1,12 - 8,5 = 13,3 - 8,5 = 4,8 м. 5. Согласно п. 8.8 необходимо также определить глубину местного размыва у подошвы насыпи, когда поток только достиг бровки берега. По формуле (8.13)
при Н = Нрбр = 4 м, υр = υрбр =
0,8 м/с, υ0 = 0,77 м/с (при глубине потока 4 м), rи = 600 м и r = 600 +
6. Поскольку полученная глубина размыва меньше рассчитанной при расчетном уровне, за искомую следует принимать h = 4,8 м. 7. Для уменьшения глубины размыва устроим срезку грунта со стороны выпуклого берега. Тогда радиус кривизны потока в русле при расчетном уровне примем равным 1,15 × rи = 1,15 × 680 » 780 м (см. п. Т.3), r = 780 + 260 / 2 = 910 м, и глубина размыва по формуле (Т.3) будет равна 2,85 м. Как видим, устройство срезки грунта на противоположном (укрепляемому) берегу является эффективным методом снижения размывов у вогнутых берегов русел. Ключевые слова: глубина местного размыва, опора моста, струенаправляющая дамба, конус моста, подошва насыпи, регуляционные сооружения, грунты связные и несвязные. СОДЕРЖАНИЕ
Нравится
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 (5.1)
(5.1)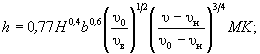 (5.2)
(5.2)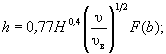 (5.3)
(5.3)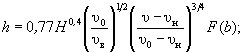 (5.4)
(5.4)
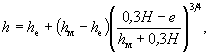 (5.6)
(5.6)
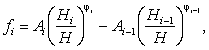 (5.10)
(5.10)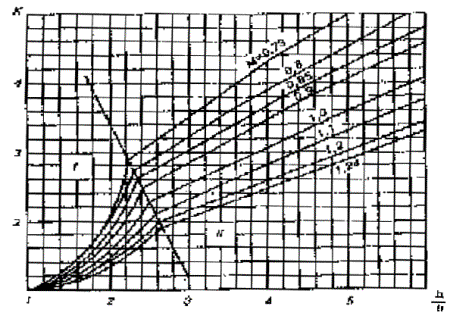
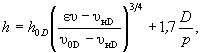 (5.15)
(5.15)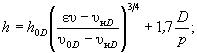 (5.16)
(5.16) (5.18)
(5.18)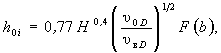 (5.19)
(5.19) (5.20)
(5.20)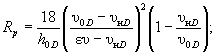 (5.23)
(5.23)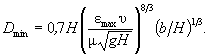 (5.25)
(5.25)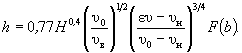 (5.26)
(5.26)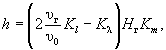 (6.1)
(6.1)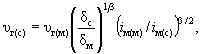 (6.4)
(6.4)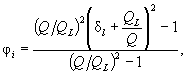 (6.9)
(6.9)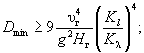 (6.14)
(6.14)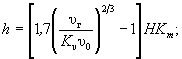 (7.1)
(7.1)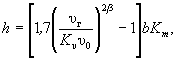 (7.2)
(7.2)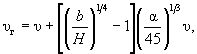 (7.4)
(7.4)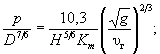 (7.7)
(7.7)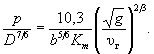 (7.8)
(7.8)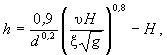 (8.1)
(8.1) (8.2)
(8.2)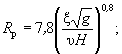 (8.4)
(8.4)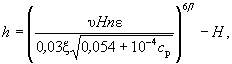 (8.6)
(8.6)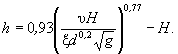 (8.8)
(8.8)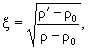 (8.9)
(8.9)
 (8.13)
(8.13) (А.2)
(А.2)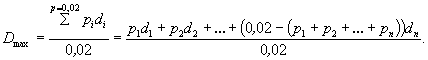 (А.4)
(А.4)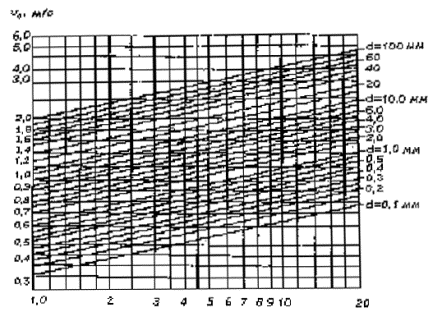

 (А.13)
(А.13)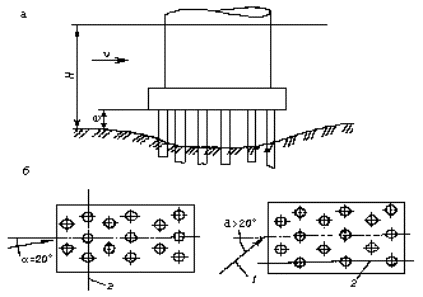
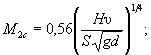 (Б.2)
(Б.2)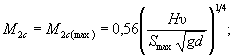 (Б.4)
(Б.4)

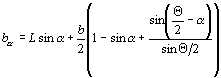
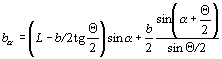

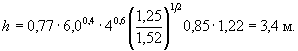
 · 2,35 = 3,28 м.
· 2,35 = 3,28 м.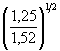 = 1,43.
= 1,43.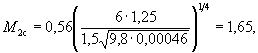
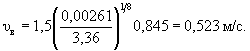
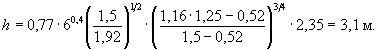
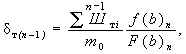 (Д.2)
(Д.2)
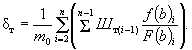 (Д.3)
(Д.3)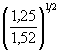 1,955 = 2,79 м.
1,955 = 2,79 м. 0,305 = 0,44 м.
0,305 = 0,44 м.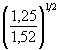 1,65 = 2,35 м.
1,65 = 2,35 м.
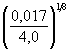 0,895 = 0,905;
0,895 = 0,905; = 3,75
= 3,75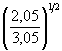 =
3,07 м.
=
3,07 м. что больше p / D
= 0,02 / 0,017 = 1,18,
что больше p / D
= 0,02 / 0,017 = 1,18,
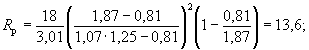
 = 3,01;
= 3,01; 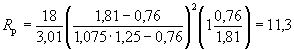 при
при 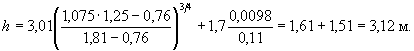
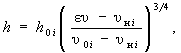 (И.1)
(И.1)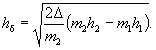 (И.2)
(И.2)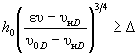 - по формуле (
- по формуле (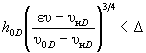 или eυ < υнD по формуле
или eυ < υнD по формуле (И.5)
(И.5) × 0,895 = 0,6 м/с.
× 0,895 = 0,6 м/с.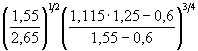 × 0,85 × 1,22 = 2,57 м.
× 0,85 × 1,22 = 2,57 м.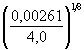 × 0,895 = 0,54 м/с.
× 0,895 = 0,54 м/с.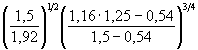 2,38 = 3,2 м.
2,38 = 3,2 м.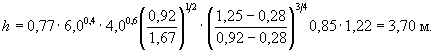
 = 0,36 м/с.
= 0,36 м/с.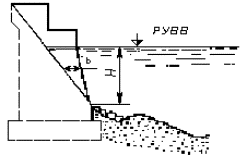
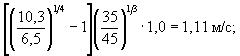
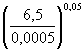 = 1,55.
= 1,55. 6,5 × 0,77 = 3,67 м.
6,5 × 0,77 = 3,67 м.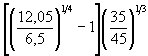 1,0
= 1,15 м/с.
1,0
= 1,15 м/с.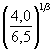 = 0,85.
= 0,85. 6,5 × 0,77 × 0,85 = 3,36 м.
6,5 × 0,77 × 0,85 = 3,36 м.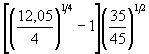 0,8 = 1,03 м/с;
0,8 = 1,03 м/с;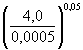 = 1,5; υ0
= 0,77 м/с, υ0 < υ < 1,35υ0;
= 1,5; υ0
= 0,77 м/с, υ0 < υ < 1,35υ0;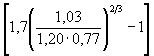 4 × 0,77 = 2,6 м.
4 × 0,77 = 2,6 м.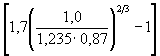 5 × 1 = 3,07 м.
5 × 1 = 3,07 м.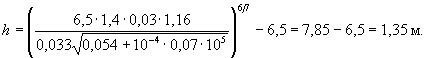
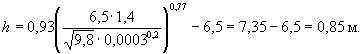
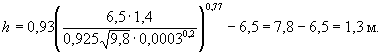
 (С.1)
(С.1)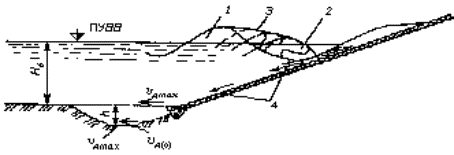
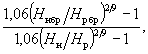 (Т.3)
(Т.3)